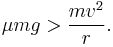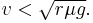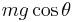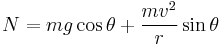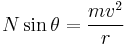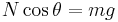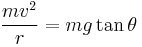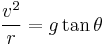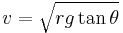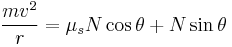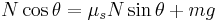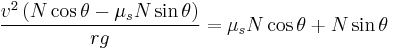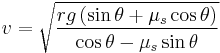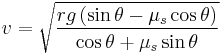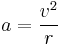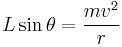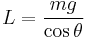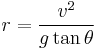Banked turn

A banked turn is a turn or change of direction in which the vehicle banks or inclines, usually towards the inside of the turn. The bank angle is the angle at which the vehicle is inclined about its longitudinal axis with respect to its path.

1 Turn on flat surfaces
2 Normal reaction in a banked turn
3 Frictionless banked turn
4 Banked turn with friction
5 Banked turn in aeronautics
6 See also
7 Notes
8 References
9 External links

Turn on flat surfaces

If the bank angle is zero the surface is flat, simplifying the calculations, and the vehicle is just driving in a circle. The normal force is vertically upwards, so the only force keeping the vehicle turning on its path is friction, or traction. This must be large enough to provide the centripetal acceleration, a relationship which can be expressed as an inequality,

$\mu mg > {mv^2\over r}.$

The expression on the right hand side is the centripetal acceleration multiplied by mass, so the force required to turn the vehicle. The left hand side is the maximum frictional force, which equals the coefficient of friction μ multiplied by the normal force. Rearranging the maximum cornering speed is

$v < {\sqrt{r\mu g}}.$

Note that μ can be the coefficient for static or dynamic friction. In the latter case, where the vehicle is skidding around a bend, the friction is at its limit and the inequalities becomes equations. This also ignores effects such as downforce which can increase the normal force and cornering speed.

Normal reaction in a banked turn

In the case of a car being parked on a banked turn, the Normal force would simply be:

$mg\cos \theta$

But once the car starts to move on a banked turn, it 'collides' with the turn itself, the turn feels this force, and returns it in the normal, causing the car to move circularly.

The Normal is thus greater than simply its gravitational component.

$N = mg\cos \theta %2B {mv^2\over r} \sin \theta$

If the Normal were simply the component to gravity, one could not say mg = Ncosθ = mgcos²θ when the vertical acceleration is 0.

Frictionless banked turn

As opposed to a car riding along a flat circle, inclined edges add an additional force that keeps the car in its path and prevents it from being "dragged into" or "pushed out of" the circle. This force is the horizontal component of the car's normal force. In the absence of friction, the normal force is the only one acting on the car in the direction of the center of the circle. Therefore, as per Newton's second law, we can set the horizontal component of the normal force equal to mass multiplied by centripetal acceleration:

$N\sin \theta ={mv^2\over r}$

Because there is no motion in the vertical direction, the sum of all vertical forces acting on the system must be zero. Therefore we can set the vertical component of the car's normal force equal to its weight:

$N\cos \theta =mg$

Solving the above equation for the normal force and substituting this value into our previous equation, we get:

${mv^2\over r}= {mg\tan \theta}$

Which is equivalent to:

${v^2\over r}= {g\tan \theta}$

Solving for velocity we have:

$v= {\sqrt{rg\tan \theta}}$

This provides the velocity that in the absence of friction and with a given angle of incline and radius of curvature, will ensure that the car will remain in its designated path. The magnitude of this velocity is also known as the "rated speed" of a turn or curve.^[1] Notice that the rated speed of the curve is the same for all massive objects, and a curve that is not inclined will have a rated speed of 0.

Banked turn with friction

When considering the effects of friction on the system, once again we need to note which way the friction force is pointing. When calculating a maximum velocity for our automobile, friction will point down the incline and towards the center of the circle. Therefore we must add the horizontal component of friction to that of the normal force. The sum of these two forces is our new net force in the centripetal direction:

${mv^2\over r}= \mu_s N\cos \theta %2BN\sin \theta$

Once again, there is no motion in the vertical direction, allowing us to set all opposing vertical forces equal to one another. These forces include the vertical component of the normal force pointing upwards and both the car's weight and vertical component of friction pointing downwards:

$N\cos \theta =\mu_s N\sin \theta %2Bmg$

By solving the above equation for mass and substituting this value into our previous equation we get:

${v^2\left(N\cos \theta -\mu_s N\sin \theta \right)\over rg}= \mu_s N\cos \theta %2BN\sin \theta$

Solving for v we get:

$v= {\sqrt{rg\left(\sin \theta %2B\mu_s \cos \theta \right)\over \cos \theta -\mu_s \sin \theta }}$

This equation provides the maximum velocity for the automobile with the given angle of incline, coefficient of static friction and radius of curvature. By a similar analysis of minimum velocity, the following equation is rendered:

$v= {\sqrt{rg\left(\sin \theta -\mu_s \cos \theta \right)\over \cos \theta %2B\mu_s \sin \theta }}$

The difference in the latter analysis comes when considering the direction of friction for the minimum velocity of the automobile (towards the outside of the circle). Consequently opposite operations are performed when inserting friction into equations for forces in the centripetal and vertical directions.

Improperly banked road curves increase the risk of run-off-road and head-on crashes. A 2% deficiency in superelevation (say, 4% superelevation on a curve that should have 6%) can be expected to increase crash frequency by 6%, and a 5% deficiency will increase it by 15%.^[2] Up until now, highway engineers have been without efficient tools to identify improperly banked curves and to design relevant mitigating road actions. A modern profilograph can provide data of both road curvature and cross slope (angle of incline). A practical demonstration of how to evaluate improperly banked turns was developed in the EU Roadex III project, see the linked referenced document below.

Banked turn in aeronautics

When a fixed-wing aircraft is making a turn (changing its direction) the aircraft must roll to a banked position so that its wings are angled towards the desired direction of the turn. When the turn has been completed the aircraft must roll back to the wings-level position in order to resume straight flight.^[3]

When any moving vehicle is making a turn, it is necessary for the forces acting on the vehicle to add up to a net inward force, to cause centripetal acceleration. In the case of an aircraft making a turn, the force causing centripetal acceleration is the horizontal component of the lift acting on the aircraft.

In straight, level flight, the lift acting on the aircraft acts vertically upwards to counteract the weight of the aircraft which acts downwards. During a balanced turn where the angle of bank is θ the lift acts at an angle θ away from the vertical. It is useful to resolve the lift into a vertical component and a horizontal component. If the aircraft is to continue in level flight (i.e. at constant altitude), the vertical component must continue to equal the weight of the aircraft. The horizontal component is unbalanced, and is thus the net force causing the aircraft to accelerate inward and execute the turn.

During a banked turn in level flight the lift on the aircraft must support the weight of the aircraft, as well as provide the necessary component of horizontal force to cause centripetal acceleration. Consequently, the lift required in a banked turn is greater than that one required in straight, level flight and can be achieved either by increasing the angle of attack of the wing (typically by pulling on the elevator control) or by deploying flaps. The maneuver is usually complemented by an increase in power, in order to maintain airspeed.

Because centripetal acceleration is:

$a = {v^2\over r}$

Newton's second law in the horizontal direction can be expressed mathematically as:

$L\sin \theta = {mv^2\over r}$

where:

L is the lift acting on the aircraft

θ is the angle of bank of the aircraft

m is the mass of the aircraft

v is the true airspeed of the aircraft

r is the radius of the turn

In straight flight, lift is approximately equal to the aircraft weight. In turning flight the lift exceeds the aircraft weight, and is equal to the weight of the aircraft (mg) divided by the cosine of the angle of bank:

$L = {mg\over{\cos \theta}}$

where g is the gravitational field strength.

The radius of the turn can now be calculated:^[4]

$r = {v^2\over{g \tan \theta}}$

This formula shows that the radius of turn is proportional to the square of the aircraft’s true airspeed. With a higher airspeed the radius of turn is larger, and with a lower airspeed the radius is smaller.

This formula also shows that the radius of turn is inversely proportional to the angle of bank. With a higher angle of bank the radius of turn is smaller, and with a lower angle of bank the radius is greater.

The angle of bank is the sole determinant of the aircraft’s load factor during the turn.

Notes

^ Beer, Ferdinand P.; Johnston, E. Russell (July 11, 2003). Vector Mechanics for Engineers: Dynamics. Science/Engineering/Math (7 ed.). McGraw-Hill. ISBN 978-0072930795.
^ D.W. Harwood, et. al., PREDICTION OF THE EXPECTED SAFETY PERFORMANCE OF RURAL TWO-LANE HIGHWAYS, Turner-Fairbank Highway Research Center, McLean, VA, December 2000, page 39, http://www.tfhrc.gov/safety/pubs/99207.pdf
^ Federal Aviation Administration (2007). Pilot's Encyclopedia of Aeronautical Knowledge. Oklahoma City OK: Skyhorse Publishing Inc.. Figure 3–21. ISBN 1602390347. http://books.google.com/books?id=m5V04SXE4zQC&pg=PT33&lpg=PT33&dq=+%22angle+of+bank%22&source=web&ots=iYTi_mZAra&sig=ytjcmr9RStdIdgZzaiBJJ-wxjts&hl=en.
^ Clancy, L.J, Equation 14.9

References

Surface vehicles

Serway, Raymond. Physics for Scientists and Engineers. Florida: Saunders College Publishing, 1996.
Health and Safety Issues, the EU Roadex III project on health and safety issues raised by poorly maintained road networks.

Aeronautics

Kermode, A.C. (1972) Mechanics of Flight, Chapter 8, 10th Edition, Longman Group Limited, London ISBN 0-582-23740-8
Clancy, L.J. (1975), Aerodynamics, Pitman Publishing Limited, London ISBN 0-273-01120-0
Hurt, H.H. Jr, (1960), Aerodynamics for Naval Aviators, A National Flightshop Reprint, Florida

External links

Surface vehicles

Aeronautics